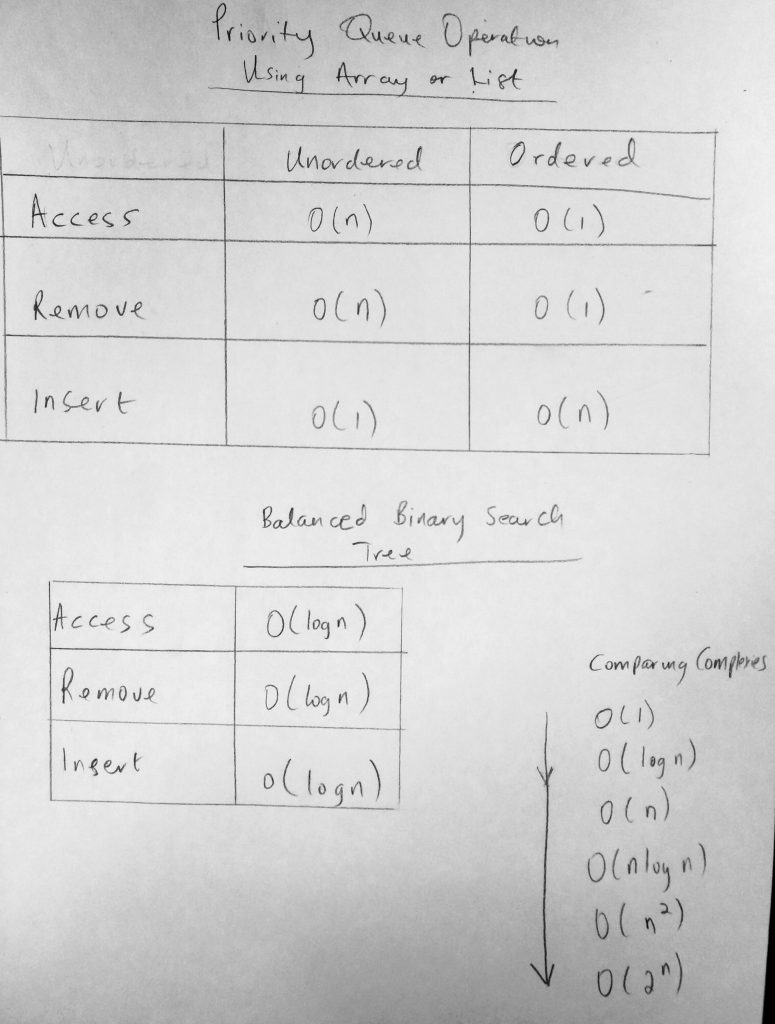
Previously in other posts (on data structures) we learned about Queues. Particularly speaking, we discussed what priority queues were. What we didn’t know is that the underlying foundation of priority queue is the heap data structure (which we will be learning about in this post). Remember that a priority queue is a data structure that allows you to access an item in a collection with the highest priority. Accessing such an item can be done in so many different ways such as using arrays or lists (binary trees being one of them). However the best way to implement priority queues is to use the heap. When accessing, inserting or deleting into such data structures, the heap is the most performant (faster than arrays/lists/binary trees). What we really didn’t talk about in that post (on queues) was runtime complexity. We implemented methods such as enqueue, dequeue, etc. but we never considered how performant they were with basic operations such as adding and removing from the queue. Lets look at a diagram.
Before we see why the Heap is so important, let us take a look at the performance of priority queues using different data structures ( see above diagram). In the first section of the diagram we are using simple lists or arrays to implement a priority queue. We look at common operations used when implementing queues such as insert, delete and remove. Our goal here in comparing, is to see which data structure does these operations as faster. The first part of the diagram uses an array or list (ordered / unordered) to perform the queue operations. Taking a look at an access operation for both ordered an unordered array/list, it makes sense that we get O(n) for unordered, since to access the element with highest priority, the collection needs to be traversed (we need to find it). However for an ordered list we know exactly where the highest priority is. Its either at the end or the beginning, making it a constant time O(1). Please take a look at remove and insert operations (they are self explanatory). As you can see there is some kind of trade off between ordered an unordered data. What if you have ordered data but you want to insert at constant time. Well that is not possible, because we have to insert the new data at the appropriate location in the ordered collection. Take not of those trade offs. Can we do better ? Yes we can by using balanced binary search trees. If you are not familiar with binary trees please read my post of them. As you are see there is a significant performance increase where all operation are at a runtime complexity of O(log n). Much better than using arrays. This is just because of the way binary trees imposes on order within a collection (to make them easily searchable). I have also provided a comparison chart for runtime complexities as an added bonus. As you can see, O(1) is the fastest, where O(2^n) is the worst. So using BST’s are better than using arrays or lists when implementing priority queues. But can we still do better? Well thats where Heaps come into place. More specifically “The Binary Heap” comes into play. Using a binary heap, we get O(log n) for insertion, O(1) for access and O(log n) for remove. As you can see its similar to BST’s but blows its away by giving an O(1) for access. This makes it the fastest out of all the data structures we have seen for implementing a priority queue. Lets dive into the heap.
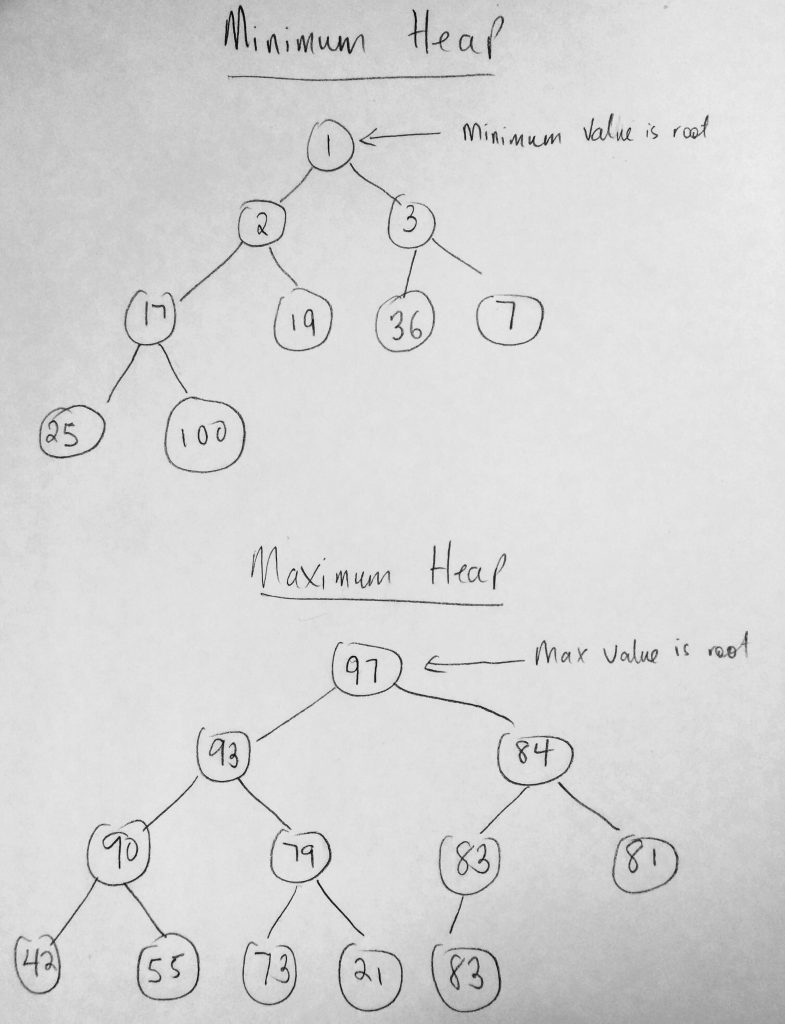
A heap is just a tree with special properties on the values of its nodes. We have already learned about the tree data structure. Just like you can have a binary tree from a tree structure, you can have a binary heap from a heap (after all a heap is just a tree). These special properties on the tree are called the “heap property”. If that property is satisfied, then that tree is a heap. There are two property types to look out for here. The first is a maximum heap, and the second is a minimum heap. A maximum heap means that the highest priority element in the queue, is the element with the highest value in the collection. A minimum heap means the element with the highest priority is the element with the lowest value in the collection. It all depends on the way you order priority in your system. If you need the highest priority to be the item with the highest value, the use a maximum heap. If you need the highest priority in your queue to be the item with the lowest number, then use a minimum heap. Its that simple. Recall the structure of the tree. If the root node is the minimum value of the collection, thats a minimum heap. The opposite is true for a maximum heap. Lets take a look at another diagram.
The above diagram describes what we have been talking about. In the minimum heap you can see that the item at the top (or root) is the highest priority. It is also the smallest item in the collection. The opposite is true for a maximum heap.
Now let us consider some characteristics of these two types of heaps. For example take a look at the minimum heap. Look at the 100 node which is a child of 17. The parent is always less than its children. 17 is less than 25 and 100. 2 which is the parent of 17 and 19 is less than both of them. The same is true for maximum heap. The parent of child nodes are greater. For example 90 is the parent of 42 and 55. 93 is the parent of 90 and 79. So every node has its values greater than its children. This is unique about the heap types. Another thing about heaps that need to be satisfied is that they should form a complete binary tree. That means that all levels except the last should be filled. That means that if the height of the tree is H, then the leaf nodes should only be at a level of H or H – 1. This is know as the shape property of a heap. The shape property MUST be satisfied as it ensures that only a complete binary tree can be a heap.
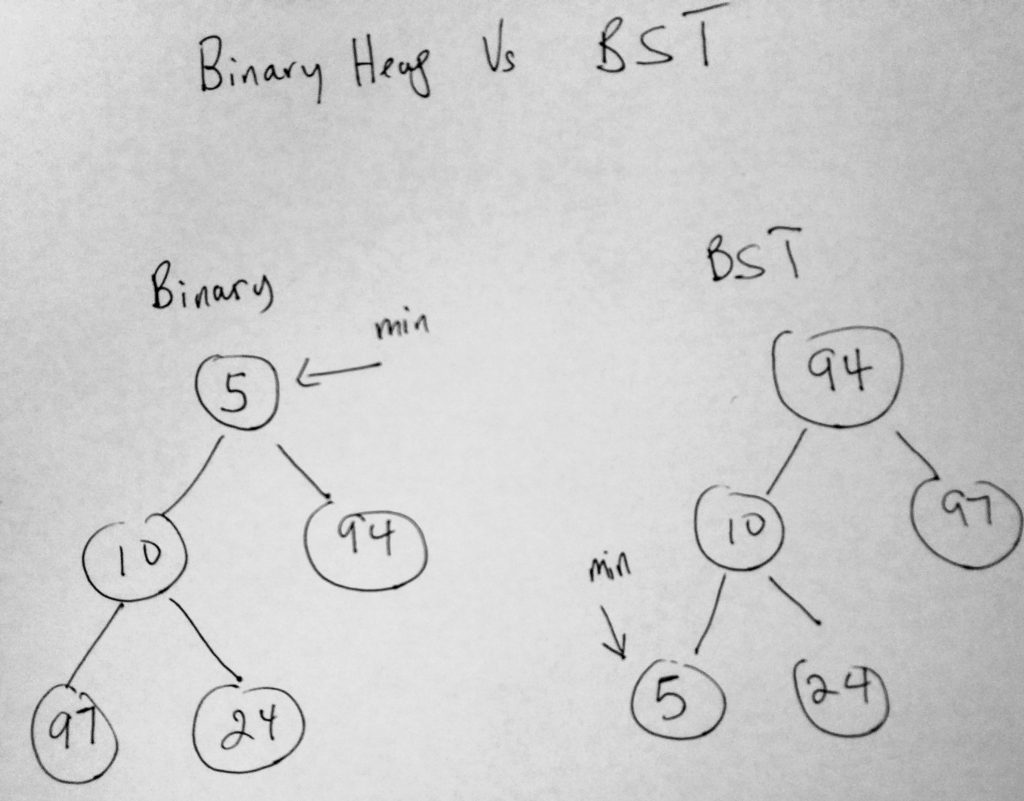
Its also important to note the differences between a binary heap and a binary search tree. If you have understood the shape property you will know that in a binary heap the parent is less than both the left and right child (in the case of a min heap), whereas in a BST the parent is greater than the left and right children.
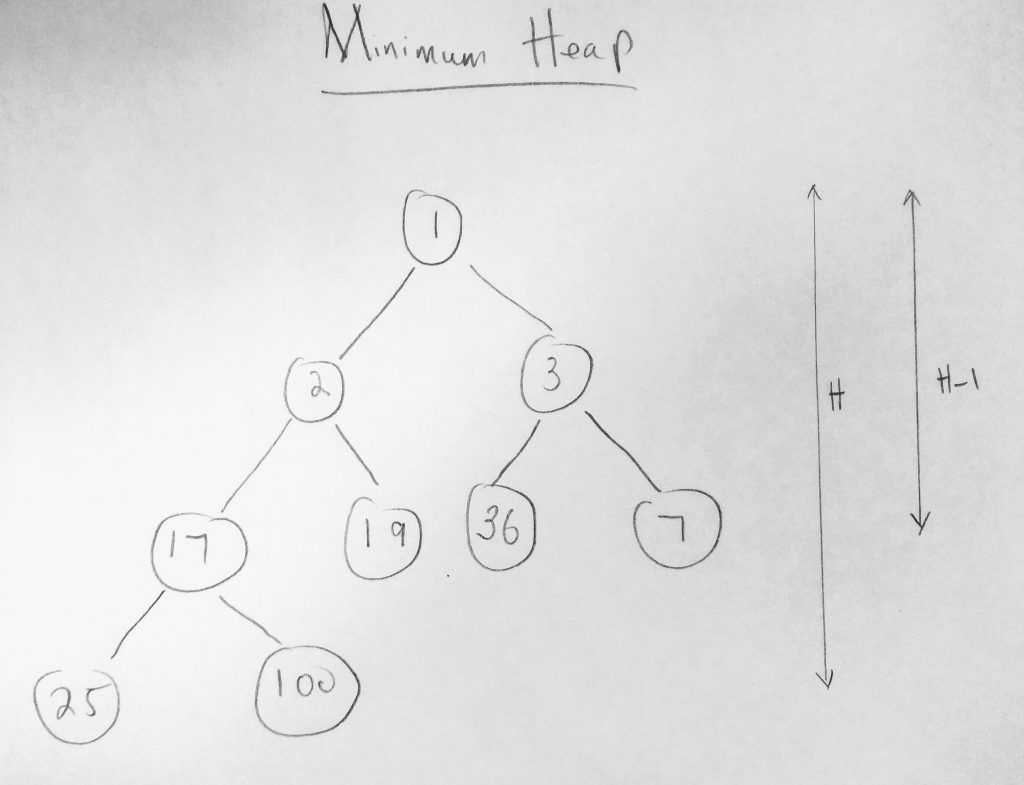
Lets expand on this shape property with yet another diagram.
Lets dive deep into satisfying the heap property. Take a look at the diagram which we saw earlier. We agreed that this is a complete binary tree and therefore a heap. In the diagram, the height of the tree is H. The nodes 25 and 100 are part of the height of the node. At H – 1, we have some leaf nodes ( 17, 19, 36, 7 ). Leaf nodes can only exist at either H or H – 1 in order to satisfy the shape property of a heap. Another thing to must be satisfied is that every level must be full. The only level that can afford not to be full is the H level. H is the only level that can be incomplete. Notice that there is space for 6 more nodes on H level. Those 6 come from being the children of 19, 36 and 7. They can all have 2 child nodes underneath them. Another thing to note is that nodes at level H – 1 have to be filled before moving to to level H. So take 25 and 100 for example. They cannot have children unless the entire H row is filled. This is what we call the shape property. So take note of these properties: the shape property and the heap property. When working with heaps these must be satisfied to proceed.
Binary Heap Implementation
We know that a heap is just a tree with special characteristics or properties. On the heap one of the operations that we would want to perform are downwards traversal. Here we can move from the root node to any leave node (trickle down). We would also like to move from any leaf node to the root node (trickle upwards). Other operations we might be interested in are, given a node, we want to know its right child, or left child, or parent node. Now if you remember when we implemented the BST, we had two properties to the left and right child pointers. Now we need to add a third pointer. For some of you this might not raise any flags. But for others you will notice right away that is is requiring more space. In a network of thousands of nodes, thats a lot of space to account for.
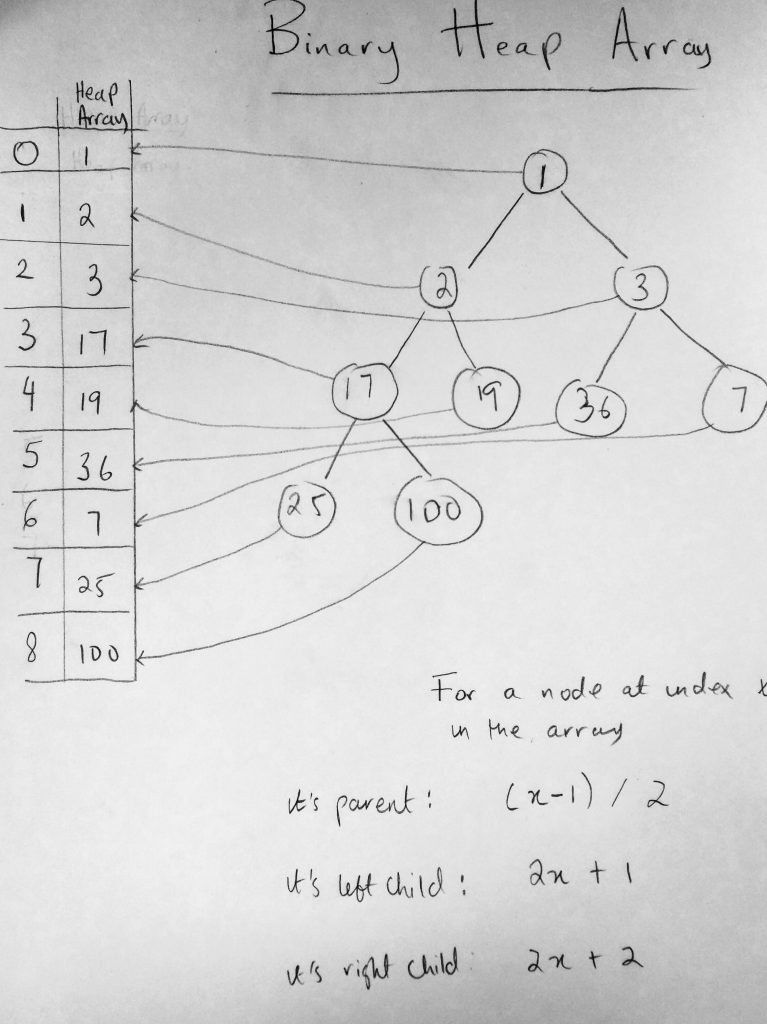
Because of this, there is a special way to represent heaps that i think is just genius! It is done using an array where the relationship between left, right and parent are all done using that very same array! We use a mathematical relationship to represent the parent and its child nodes (replacing the pointer approach – new property to the class). Remember we talked about heap properties where every level must be filled, etc. Well we use array indices to represent the levels using this methodology. Note that this approach is not the same as the first approach we talked about (implement priority queues with arrays, we are still taking about using heaps to build priority queues uses binary trees represented by arrays using a special relationship mapping. The best way to understand this is to look at a diagram.
Neat huh? Here we have a binary tree or a heap that has been transformed into an array(so its no ordinary array). We are using arrays to represent the heap with the help of a mathematical relationship. On the left we have the array index slots with their heap or tree value. So for example at index 0 we have the value of 1 (which is the root node). Now closer to the end of the diagram i have a formula that you can use to map your heap value to an array index! For a node at index X in the array, we have a mathematic relationship to find out where its value should be in the array. For example in the diagram, notice that index 1 and 2 have the values of 2 and 3 respectively. Why wasn’t it the other way around ( 3 and 2). Well for a node at index x, to find the right child, we use the 2x + 1 formula to get which slot it should be. Node 2 and 3 are the left and right children of node 1. We can choose to place node 1 anywhere we like in our array. We choose to put it at index 0. So using the formula 2(0) + 1 = 1 for the left child (which means place 2 in index 1), and 2(0) + 2 = 2 for the right child, which means place 3 at index 2! Lets take another example. We just placed node 3 at index 2. Lets see where to place the children of node 3. For the left child, 2(2) + 1 = 5 and the right child 2(2) + 2 = 6. So that means place 36 on the left of 3 and 7 at the right. Voila! We can do the same thing to get the parent element slot. However notice that we will have to use the Math.floor method to round the number down. To get the parent of node 2 and 3 which are at indices 1 and 2, we do (2 – 1) / 2 = 0.5 (then we round down to 0). That means the parent index of 2 and 3 should be at index 0. Its like genius magic!
Now that we know how to use an array to represent a binary heap using a relationship, let us start talking about code implementation. Earlier on we learned about minimum and maximum heaps. Lets see how we are going to put everything together. We will be writing a base class that houses commonalities between the two types of heaps. We implement methods such as swap, get left, right and parent node indices, check the size of the collection. And then write the min and max heap class to inherit from the base class.
Heapify
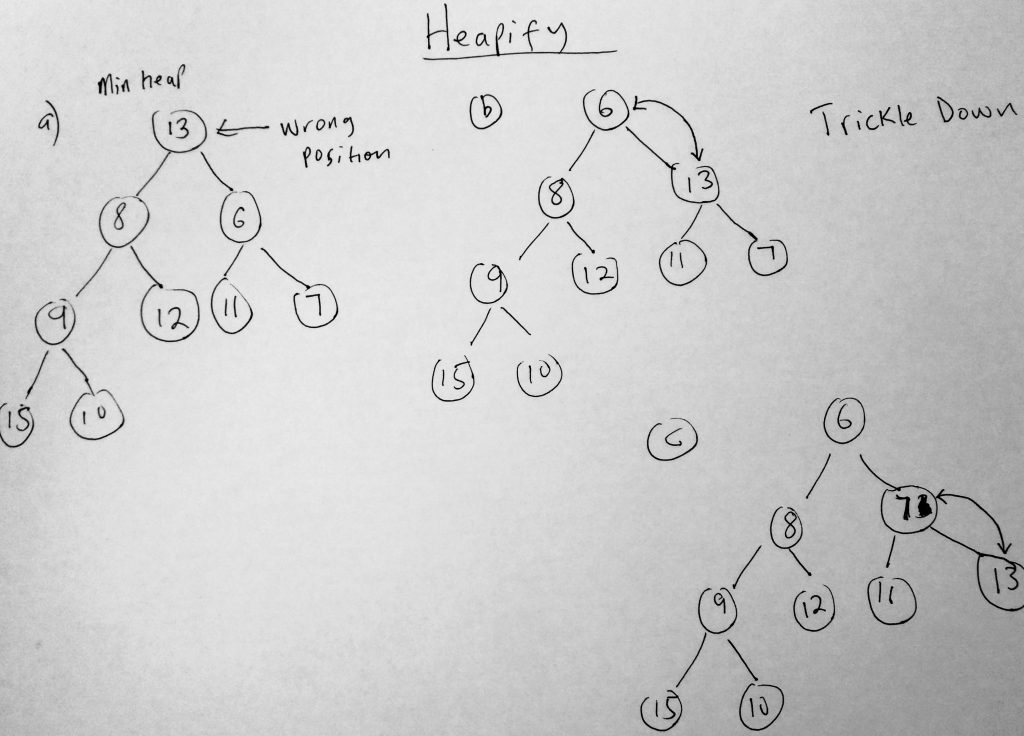
In our implementation of our binary heap, three very important methods we need to speak about are inserting into the heap, getting the highest priority element, and removing from the highest priority from the heap. The way we do these, is to create some helper methods in our two heap types to help make these operations possible. We call these operations, heapify operations. Depending on the type of heap you are creating, our insert method has a trickle up method which helps bubble the element that was just inserted to the right position of the heap. The algorithm works like this. When you insert a new element to the heap, it adds that element at the end of the heap (in this case last element in the array – note: which might probably be the wrong position) and then it calls a trickleup method which is a recursive function. What it does is check to see if the node just added has a parent, and thus gets its parent index. It checks to see if its value is bigger than the parent and depending on whether it is or not, it will swap values. It keeps doing this until it finds it rightful place in the heap data structure (pretty neat huh). Removing the element with the highest priority, is done by first getting the highest priority and then calling a trickledown method, to bubble down the heap (which ends up reshuffling and rearranging itself). First the highest priority is removed from the top, and the last element in the array is put to the first position. After this happens a recursive function is called to reorganize elements into their right positions. Remember heap here refers to an array with a special relationship model. This might all sound confusing, lets take a look at a diagram of what trickleup and trickledown are doing. May it might help clarity a little (this is pretty advanced if you ask me).
The diagram above tries to explain what happens when an element is added to the heap. In this case this is a min heap. Notice that this means that the smallest number should be at the root. But 13 is definitely not the smallest number. Because of this we call the heapify operation trickledown to do its work. It checks to see the two child nodes (left and right). Finds the smaller of the two (6), and swaps itself with that element (#b). Since this is recursive, it keeps going. It checks to see if the heap property is satisfied by checking the child nodes again. 7 is the lesser of the child nodes to we swap again in #C. There is also a trickle up operation, its the reverse of what you have seen above.
In the case of both minimum and maximum heap types, adding a new node of elements, adds it to the end of the array. When that happens its bubbles up the heap to its rightful place. This means that as we keep adding to the heap, its keeps organizing itself and always has the highest priority at the top. Because of this removal of the highest priority if very fast at O(1). Insertion and deletion are also very fast at O(l0g n). When we insert, we do so by adding to the end of the array and then finding the right place for the element in the heap. Even though we can delete the highest priority immediately we have to re-heapify the elements, and that takes log n time.
Lets take a look at some code that might shed more light on the matter.
Base Class
Lets write our base heap class and put in some of these methods we are talking about, like get left, right and parent node. We will first implement a base heap class that will be inherited by a minimum and maximum heap class. The base class will house the common methods. Please note that the ES2015 versions are located on github.
See the Pen Heap Base by kofi (@scriptonian) on CodePen.
Maximum and Minimum Heap
Maximum and Minimum Heap are subclasses of Heap. In these Classes we write our helper methods to insert and remove priorities from the head. So pretty much this is where we write our heapify operations.
First Max Heap:
See the Pen Max Heap by kofi (@scriptonian) on CodePen.
Next Min Heap:
See the Pen Min Heap by kofi (@scriptonian) on CodePen.
Ok thats a lot of code right there. By this point i assume you are all at least intermediate javascript developers and are family with object oriented javascript. If you are not i highly suggest you read my post on the subject matter. Please note i wasn’t using codepen and gist to write code back then, so there are some code formatting issues (nothing that will hold you back though, but be prepared to see these – working on updating all those posts to use code pen for writing code).
Our base class has methods that our subclasses will use. Notice that insert and removeHighest priority can only be called from the subclass (Minheap & Maxheap). Since these classes inherit functionality from the parent class, when we instantiate them we pass in the size of the heap we want to create. The subclass calls the parent class to get this done. There is nothing complex going on in the base class. Take a look at the get parent, left and right child index methods. These use the mathematical relationship we spoke about. Everything being done here we have talked about so its not necessary to say again. When we call our heapify methods, some of these helper classes are involved. Notice that both min and max heap class implement their own versions of insert and removeHighest priority. In an ideal world these should really be in the base class, so you can refactor them if you like. The only thing you would have to do is find a way to call the subclasses methods from within the parent class (javascript doesnt make it too easy). So refactor them yourself if you like. This is surely make your subclasses a bit leaner. When insert is called in either class, it first checks to make sure that the collection is not full (if so throws and error). If its not full it adds the element to the end of the array and then calls the trickleup heapify method which recursively puts that element in the right location. The implementation for trickleDown is also very similar (but not the same) across subclasses. This function is called when removeHighestPriority is called. This action starts from the first item in the array and then puts the element into its right place.
The heap data structure is the best way to implement priority queues. We learned that using arrays is the best way of implementing a binary heap data structure (instead of the using arrays and the QueueItem object we used in the previous post). We also talked about runtime complexity (see diagram above). The binary heap data structure out performs other structures by doing insert, access and remove operations at O(log n), O(1) and O(log n) respectively. Thanks for reading. Feel free to reach out on twitter as well ( @scriptonian ) if you have any questions.